Authors: Louis Vignoli
Quantum computing can be approached through multiple paradigms, each with its own strategy for handling errors. Analog quantum computing leverages the natural evolution of quantum systems and can exhibit resilience to certain types of noise. Digital quantum computing, by contrast, relies on discrete operations, where errors must be actively managed to avoid failure. These aren’t fundamentally different machines, but rather different ways of harnessing the same quantum hardware.
At Pasqal we focus on two key paradigms: analog quantum computing for near-term applications, and fully digital systems designed to support quantum error correction. While each paradigm has its strengths, one truth remains: digital quantum computing cannot succeed without robust error management.
Measurement Precision vs. Computing Challenges
Quantum mechanics is the most accurate tool for describing how nature works, with its success extending far beyond laboratories. Atomic clocks, based on quantum principles, define time with impressive precision, making technologies like GPS possible.
One of quantum physics’ major achievements is quantum electrodynamics. It allows scientists to predict an electron’s magnetic properties with accuracy to one part in a trillion–a testament to the power of our physical theories.
Yet when we build quantum computers, we find ourselves battling errors at every turn. Why does this paradox exist? Where do these errors come from? And what can we do about them?
The Delicate Nature of Quantum Computing
At the core of a quantum computer is the qubit, the quantum counterpart of the classical bit (0 or 1). Unlike classical bits, qubits can exist in a superposition of multiple states at once, opening the door to vast computational possibilities.
At Pasqal, we create qubits – quantum versions of classical bits – by trapping individual Rubidium-87 atoms. Using lasers, we control just one of the atom’s 37 electrons, the valence electron – the outermost and most loosely bound electron, making it highly responsive to external control. Though this electron has a theoretically infinite number of discrete states, we deliberately restrict it to only two levels.
This task is challenging because quantum states are inherently delicate and highly sensitive to their environment. Imagine trying to balance a pencil on its tip while:
- The table occasionally vibrates
- Tiny air currents brush against the pencil
- The temperature fluctuates slightly
- Someone occasionally bumps your elbow
This is the challenge of quantum computing. The tiniest environmental disturbance – a subtle temperature change, a stray electromagnetic wave, or even the quantum system’s interaction with itself – can disrupt the delicate quantum state, a problem known as “decoherence.”
From One Qubit to Many: Errors Multiply
A single qubit, though impressive to create, isn’t computationally useful on its own. The real power emerges when multiple qubits work together. On neutral-atom platforms, where thousands of atoms can be trapped simultaneously, multi-qubit controlled behavior is enabled by exploiting a phenomenon known as the Rydberg blockade. For a deeper dive, explore our Quantum Computing with Neutral Atoms white paper.
Having many qubits compounds our challenges:
- Each qubit must be individually controlled with extreme precision
- Qubits must interact in carefully orchestrated ways
- These interactions themselves can introduce errors
- Every qubit adds more potential points of failure
These errors come from two main sources: imperfect control operations as we manipulate the qubits and environmental noise that we can’t completely eliminate.
Despite the presence of many errors, a key aspect is that they typically remain local, affecting only a small part of the system rather than immediately corrupting all qubits. This locality is crucial because it allows us to design strategies to detect and mitigate errors before they spread uncontrollably.
Building Robustness to Errors
As of today, errors in quantum computing systems are inevitable. Given how fragile quantum states are when imperfectly isolated, hardware improvements alone will likely be insufficient to reduce errors to rates that enable reliable quantum computing.
Hence, robust computing solutions are necessary to handle infrequent but inevitable local errors. As Daniel Gottesman, one of the pioneers of Quantum Error Correction, put it: “Our goal is to produce protocols which continue to produce the correct answer even though any individual component of the [quantum] circuit may fail.” (Read the full article here)
This concept is known as fault tolerance. A core tenet of fault tolerance is to limit the impact of these infrequent but inevitable local errors by preventing them from spreading across the whole quantum system. Anticipating a bit, this will make errors much easier to correct.
Let’s illustrate error proliferation with a simple case. The following circuit (Fig. 1) prepares a GHZ state on four qubits. A GHZ state (named after Greenberger, Horne, and Zeilinger) is a specific type of entangled state where all qubits are correlated with each other in a superposition. This means that the state of each qubit is directly linked to the states of the others. How reliable is it? How robust is it to errors?
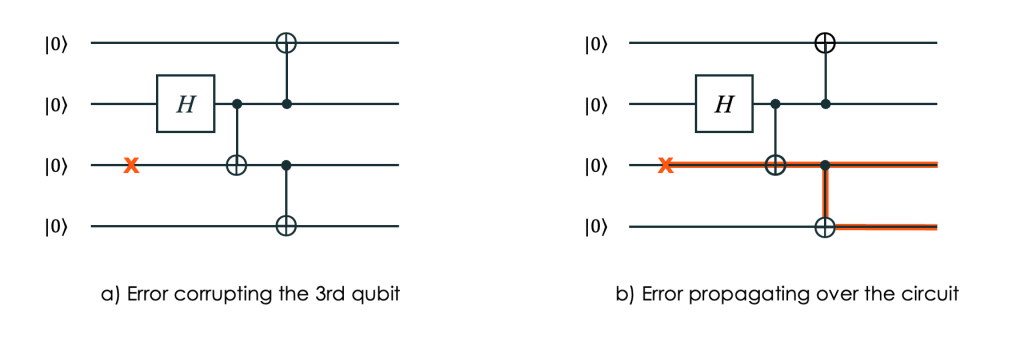
b) Same circuit with an X error. Lanes in red show how the error spreads and which qubits suffer from bit-flip in the end.
Consider a bit-flip error on a single qubit, also called an X error. Suppose qubit 3 experiences an X error after initialization and before any two-qubit gates, as shown in Fig. 1. Tracing this error through the circuit, we see that the final state is affected on two of its qubits, becoming instead of
. Hence, a single qubit error has spread across the quantum system, corrupting it extensively.
A simple way to allow detection of such serious errors is to add an ancilla qubit entangled with the first and fourth data qubits after the GHZ state preparation (Fig. 2). The previous X error now also flips the ancilla qubit. By measuring the ancilla qubit, we can detect this error! Note that the specific way the ancilla is entangled with the data qubits is carefully chosen to reveal errors in the GHZ state (for reasons not described here).
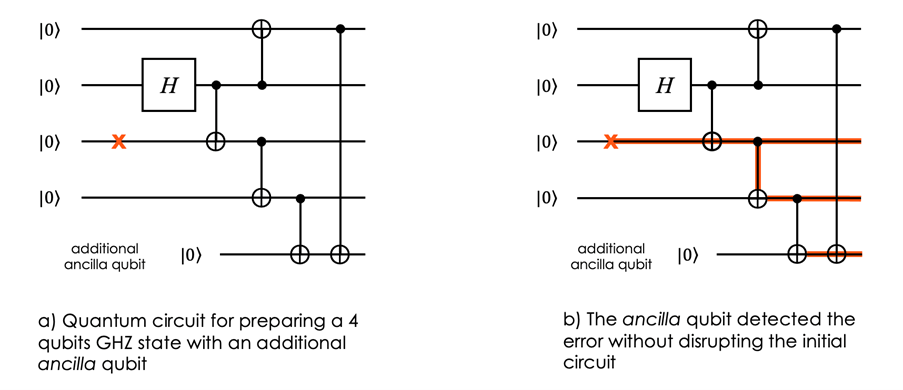
b) How the X error from Fig 1 is now detected by the ancilla qubit.
This flag-based method is a simple trick to engineer some robustness. It does not tell us what error happened or how to correct it, but it flags some situations where the state is heavily corrupted, indicating that we should discard it and try preparing a new one.
Quantum Error Correction
Now, to be properly robust to errors, it’s not enough to limit their proliferation: we need a way to correct some of them without disrupting the quantum computation. Hence, the foundation for engineering generic fault tolerance in quantum computations is Quantum Error Correction (QEC).
The breakthrough approach in QEC is that quantum information can be protected by distributing it across an entangled system. When errors occur, they don’t destroy the information but instead transform it in ways that can be identified and reversed through carefully designed measurements and corrective operations.
Think of it like composing a symphony, where the melody isn’t carried by a single instrument but spread across an entire orchestra.
Even if one instrument gets detuned, the overall melody remains mostly intact. The conductor can hear the mistake and get the musician to retune their instrument to match the orchestra.
Unlike classical error correction, QEC must overcome the no-cloning theorem (the impossibility of making perfect copies of quantum states) and perform error detection – extract information about the location of potential errors – without directly measuring the protected quantum information (which would destroy the quantum state during computation).
The development of practical QEC represents one of quantum computing’s greatest challenges and opportunities – turning quantum fragility into computational power through clever engineering.
Fault tolerance isn’t just a technical detail – it’s the key to unlocking quantum computing’s full potential.
The future of quantum computing won’t be built on perfect components, but on clever systems that remain reliable even when individual parts fail – turning quantum computing’s greatest challenge into its most impressive engineering triumph.
This post is part of a series exploring quantum computing fundamentals. Watch for our upcoming deep dive into neutral-atom based quantum error correction and fault-tolerant quantum computing
